为了鉴别词性,需要使用神经元网络对结果进行选择。这里介绍以下比较最典型的BP神经网络。
如下图所示,这是一个典型的三层神经网络结构,第一层是输入层,第二层是隐藏层,第三层是输出层。
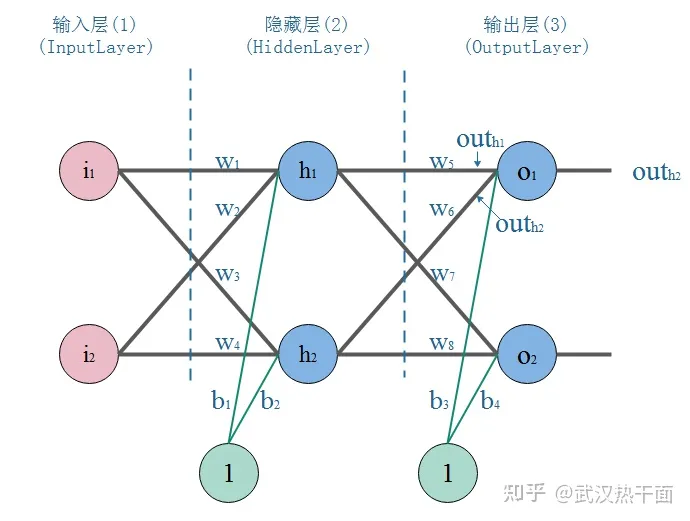
训练模型的步骤是:
(1)正向传播:把点的坐标数据输入神经网络,然后开始一层一层的传播下去,直到输出层输出结果。
(2)反向传播:始根据数据误差调整各个部分的权重\(w_i\)和偏置\(b_j\)。
(3)当完成了一次正反向传播,也就完成了一次神经网络的训练迭代。反复迭代,误差越来越小,函数的判断也就越来越精准。
1 函数
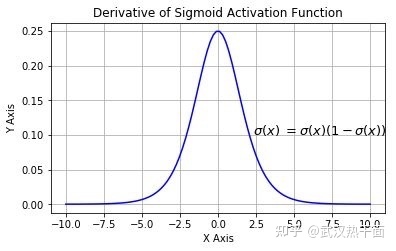
在谈到神经网络的时候,需要用到两个函数:Sigmoid函数及其导数函数。
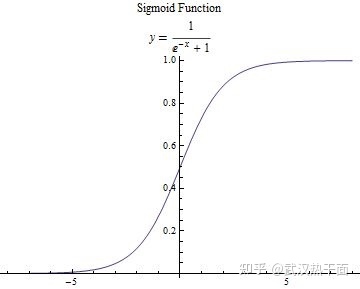
\[y(x)=\frac {1}{e^{-x} + 1}\]
\[y^{‘}=\frac {d}{dx}(\frac {1}{e^{-x} + 1})=y(x)\cdot [1-y(x)]\]
2 正向传输
正向传输的步骤相对比较容易理解和实现:
\[in_{h_j} = \sum \limits_{i=1}^N w_i \cdot i_i + b_j\]
\[out_{h_j} = y(in_{h_j})=\frac {1}{e^{-in_{h_j}}+1}\]
其中\(j\)为隐藏层的编号,\(in_{h_j}\)为隐藏层的输入数据。\(N\)为输入端个数。
\[in_{O_k} = \sum \limits_{i=1}^M w_i \cdot out_{h_j} + b_k\]
\[out_{O_k} = y(in_{O_k})=\frac {1}{e^{-in_{O_k}}+1}\]
其中\(k\)为输出层的编号,\(in_{O_k}\)为输出层的输入数据。\(M\)为输入端个数。
3 误差计算
\[E=\sum \limits_{i=1}^L E_{O_i} \\ = \frac {1}{2}{ (e_{O_1}-out_{O_1})}^2 + \frac {1}{2}{ (e_{O_2}-out_{O_2})}^2 + …… \]
其中\(E\)为总误差量,时用来检测总体收敛情况。\((e_{O_i}-out_{O_i})\)是误差分项。\(e_{O_i}\)为期望值的分项,\(L\)为输出层个数。
4 反向传播
反向传播的步骤相对比较有难度,需要有一定的高数基础。主要是用到了导数,以及链式法则。
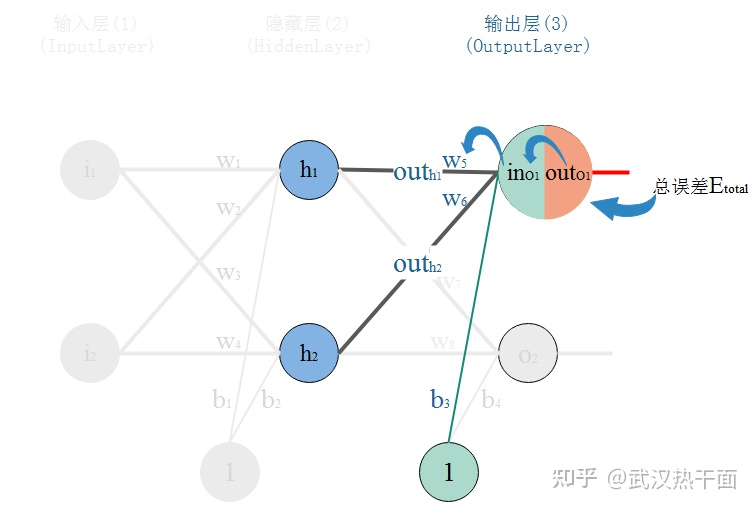
以\(w_5\)为例:
\[\frac {\partial E }{ \partial w_5 } = \frac {\partial E }{ \partial out_{O_1}} \cdot \frac {\partial out_{O_1}}{\partial in_{O_1}} \cdot \frac {\partial in_{O_1}}{\partial w_5} \]
(1)因
\[E=\sum \limits_{i=1}^L E_{O_i} \\ = \frac {1}{2}{ (e_{O_1}-out_{O_1})}^2 + \frac {1}{2}{ (e_{O_2}-out_{O_2})}^2 + …… \]
所以
\[ \frac {\partial E}{\partial out_{O_1}} = 2 \cdot \frac {1}{2} \cdot (e_{O_1} – out_{O_1}) \cdot (-1) = – (e_{O_1} – out_{O_1}) \]
(2)因
\[out_{O_1} = y(in_{O_1})=\frac {1}{e^{-in_{O_1}} + 1}\]
所以
\[ \frac {\partial out_{O_1}}{\partial in_{O_1}} = y^{‘} (in_{O_1}) = y(in_{O_1})[1-y(in_{O_1})] = out_{O_1}(1-out_{O_1})\]
(3)因
\[in_{O_k} = \sum \limits_{i=1}^M w_i \cdot out_{h_j} + b_k\]
所以
\[\frac {\partial in_{O_1}}{\partial w_5}=out_{h_1}\]
(4)于是
\[\frac {\partial E}{\partial w_5} = \frac {\partial E}{\partial out_{O_1}} \cdot \frac {\partial out_{O_1}}{\partial in_{O_1}} \cdot \frac {\partial in_{O_1}}{\partial w_5} \\ = -(e_{O_1} – out_{O_1})\cdot out_{O_1}(1-out_{O_1})\cdot out_{h_1} = \sigma_{O_1} \cdot out_{h_1} \]
其中\(\sigma = -(e_{O_1}-out_{O_1})\cdot out_{O_1}(1-out_{O_1})\)。
则对于\(b_3\)同样可以推导出:
\[\frac {\partial E}{\partial b_3} = \frac {\partial E}{\partial out_{O_1}} \cdot \frac {\partial out_{O_1}}{\partial in_{O_1}} \cdot \frac {\partial in_{O_1}}{\partial b_3} = \sigma_{O_1}\]
设神经网络的学习率为\(\alpha\),更新输出层的权重和偏置:
\[{w_i}^{‘}= w_i – \alpha \cdot \frac {\partial E}{\partial w_i}\]
\[{b_j}^{‘}= b_j – \alpha \cdot \frac {\partial E}{\partial w_j}\]
其中\(i\)为输出层的权重编号,\({w_i}^{‘}\)为更新后的权重;\(j\)为输出层的偏置编号,\({b_j}^{‘}\)为更新后的偏置。
以上仅完成了从输出到隐藏层的反向传播计算,下面要完成从隐藏层到输入层的反向传播计算。
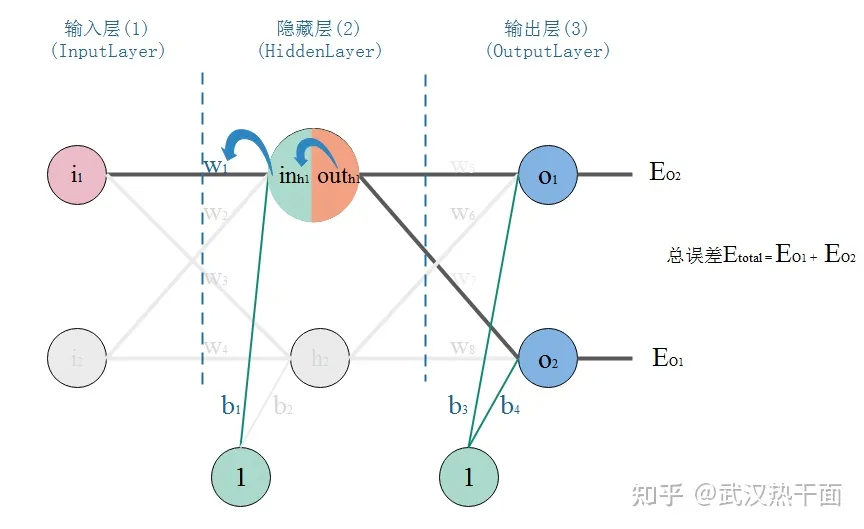
以\(w_1\)为例:
\[\frac {\partial E}{\partial w_1} = \frac {\partial E}{\partial out_{h_1}} \cdot \frac {\partial out_{h_1}}{\partial in_{h_1}} \cdot \frac {\partial in_{h_1}}{\partial w_1} \\ = (\frac {\partial E_{O_1}}{\partial out_{h_1}}+\frac {\partial E_{O_2}}{\partial out_{h_1}})\cdot \frac {\partial out_{h_1}}{\partial in_{h_1}} \cdot \frac {\partial in_{h_1}}{\partial w_1}\]
(1)可以先计算
\[\frac {\partial E_{O_1}}{\partial out_{h_1}} = \frac {\partial E_{O_1}}{\partial in_{O_1}} \cdot \frac {\partial in_{O_1}}{\partial out_{h_1}} \\ = (\frac{\partial E_{O_1}}{\partial out_{O_1}} \cdot \frac{\partial out_{O_1}}{\partial in_{O_1}})\cdot \frac {\partial in_{O_1}}{\partial out_{h_1}} \\ = -(e_{O_1} – out_{O_1}) \cdot (1-out_{O_1})\cdot w_5 = \sigma_{O_1} \cdot w_5\]
同理可得
\[\frac {\partial E_{O_2}}{\partial out_{h_1}}= \sigma_{O_2} \cdot w_7\]
(2)\(\frac {\partial out_{h_1}}{\partial in_{h_1}}=out_{h_1}(1-out_{h_1})\)
(3)\(\frac {\partial in_{h_1}}{\partial w_1} = \frac {\partial}{\partial w_1}(\sum \limits_{i=1}^N w_i \cdot i_i + b_j)=i_1\)
所以
\[\frac {\partial E}{\partial w_i} = \sum \limits_{i=1}^N \frac {\partial E_{O_i}}{\partial out_{h_i}} \cdot \frac {\partial out_{h_1}}{\partial in_{h_1}} \cdot \frac {\partial in_{h_1}}{\partial w_1} \\ = (\sum \sigma_O w_O) \cdot out_{h_i} (1-out_{h_i})\cdot i_i \]
令\(\sigma_{h_i} = (\sum \sigma_O w_O) \cdot out_{h_i} (1-out_{h_i})\),则\(\frac {\partial E}{\partial w_i} = \sigma_{h_1}\cdot i_i\)。
可以推导得:\(\frac {\partial E}{\partial b_i}=\sigma_{h_1}\)。读者比较两层的反向传播公式,就可以看出一些相似性。
这一段符号比较多,有点眼花缭乱。读者可以试着这样理解:
(1)把整个神经网络反向运行,输入看作输出,输出看作输入。
(2)在反向运行状态下,误差\(\sigma\)就是输入端的原始数值。
输入误差的公式为:\(\sigma_{O_i}=-(e_{O_i}-out_{O_i})\cdot out_{O_i}(1-out_{O_i})\)。这里不用执着于下标,每个原神经网络的输出端仅能对应一个误差。这个是“一一对应”的关系,不会出错。
此时可以根据公式(含学习率)可以更新权重和偏置。权重的更新,与权重所在的连接有关。将误差\(\sigma\)与权重所连接的另外一端输入值相乘即可。偏置仅与误差\(\sigma\)相关。
(3)在反向运行状态下,将误差传递至隐藏层。
此时,应以各个原输出节点的误差作为输入,即:误差\(\sigma\)作为隐藏层的输入。各个误差加权求和后,乘上隐藏层节点的导数数值,可以构成新的误差。此新构成的误差与原输入节点相乘,即可得到修正各权重的数值。
\(w_2\)两端连接着\(i_2\)和\(h_1\)。所以\(w_2\) 的误差输入就与\(w_5\)和\(w_7\)相关。弄清楚相关关系后,就可以按照公式进行计算。
\(b_2\)连着\(h_2\),节点\(h_2\)又通过\(w_6\)和\(w_8\)连接着输出端。这样就理顺了误差传播的途径关系,然后按照公式进行计算即可。
如果读者还有疑问,可以参考更详细的文章《BP神经网络算法推导及代码实现笔记》。
如下代码是BP神经网络的代码。仅两层,全连接,但是对输入、输出和隐藏层节点数可调。Main函数是检查代码正确性的标定代码。由于浮点运算的误差,因此只要数值很接近就足矣。
using System;
using System.Diagnostics;
namespace NLP
{
public class BPNetwork
{
// 学习率
public double LearningRate { get; set; } = 0.618f;
// 输入层
private int InputCount;
#if _USE_CLR
private double[] Inputs;
#elif _USE_CONSOLE
private double[]? Inputs;
#endif
// 隐藏层
private int HiddenCount;
#if _USE_CLR
private double[] Hiddens;
#elif _USE_CONSOLE
private double[]? Hiddens;
#endif
// 输出层
private int OutputCount;
#if _USE_CLR
private double[] Outputs;
#elif _USE_CONSOLE
private double[]? Outputs;
#endif
// 误差
#if _USE_CLR
private double[] Errors;
#elif _USE_CONSOLE
private double[]? Errors;
#endif
// 偏置
#if _USE_CLR
private double[] InputBiases;
private double[] OutputBiases;
#elif _USE_CONSOLE
private double[]? InputBiases;
private double[]? OutputBiases;
#endif
// 误差
// 反向传播计算
#if _USE_CLR
private double[] Deltas;
#elif _USE_CONSOLE
private double[]? Deltas;
#endif
// 输入层权重
#if _USE_CLR
private double[][] InputWeights;
#elif _USE_CONSOLE
private double[][]? InputWeights;
#endif
// 输出层权重
#if _USE_CLR
private double[][] OutputWeights;
#elif _USE_CONSOLE
private double[][]? OutputWeights;
#endif
public BPNetwork()
{
}
public int GetInputCount()
{
return InputCount;
}
public int GetOutputCount()
{
return OutputCount;
}
public int GetHiddenCount()
{
return HiddenCount;
}
static double Sigmoid(double x)
{
// 返回结果
return 1.0f / (1.0f + Math.Pow(Math.E, -x));
}
static double DeltaSigmoid(double x)
{
double value = Sigmoid(x);
// 返回结果
return value * (1.0f - value);
}
public void Initialize(int InputCount, int OutputCount, int HiddenCount)
{
#if DEBUG
Debug.Assert(InputCount > 1);
Debug.Assert(OutputCount > 0);
Debug.Assert(HiddenCount > 1);
#endif
// 设置输入层
this.InputCount = InputCount;
// 设置输出层
this.OutputCount = OutputCount;
// 设置隐藏层
this.HiddenCount = HiddenCount;
// 创建输入数据
Inputs = new double[InputCount];
// 创建输出数据
Outputs = new double[OutputCount];
// 创建隐藏层数据
Hiddens = new double[HiddenCount];
// 创建误差数据
Errors = new double[OutputCount];
// 创建误差数据
Deltas = new double[OutputCount];
// 创建偏置数据
InputBiases = new double[HiddenCount];
// 创建输入层权重
InputWeights = new double[HiddenCount][];
for (int i = 0; i < HiddenCount; i++)
{
InputWeights[i] = new double[InputCount];
}
// 创建偏置数据
OutputBiases = new double[OutputCount];
// 创建输出层权重
OutputWeights = new double[OutputCount][];
for (int i = 0; i < OutputCount; i++)
{
OutputWeights[i] = new double[HiddenCount];
}
// 给定一个初始值
Random random = new Random((int)DateTime.Now.Ticks);
// 随机给定数值
for (int i = 0; i < InputCount; i++)
Inputs[i] = random.NextDouble();
for (int i = 0; i < OutputCount; i++)
Outputs[i] = random.NextDouble();
for (int i = 0; i < HiddenCount; i++)
for (int j = 0; j < InputCount; j++)
InputWeights[i][j] = random.NextDouble();
for (int i = 0; i < OutputCount; i++)
for (int j = 0; j < HiddenCount; j++)
OutputWeights[i][j] = random.NextDouble();
}
public double[] GetOutputs()
{
#if DEBUG
Debug.Assert(Outputs != null);
#endif
return Outputs;
}
public void SetInputs(double[] Inputs)
{
#if DEBUG
Debug.Assert(this.Inputs != null);
Debug.Assert(Inputs != null &&
Inputs.Length == this.InputCount);
#endif
// 拷贝数据
Inputs.CopyTo(this.Inputs, 0);
}
public double GetError()
{
#if DEBUG
Debug.Assert(Errors != null);
#endif
// 数值
double value = 0.0;
// 循环处理
for (int i = 0; i < OutputCount; i++)
{
// 误差求和
value += 0.5 * Errors[i] * Errors[i];
}
// 返回结果
return value;
}
public void SetOutputs(double[] expects)
{
#if DEBUG
Debug.Assert(Errors != null);
Debug.Assert(Outputs != null);
Debug.Assert(expects != null &&
expects.Length == this.OutputCount);
#endif
// 循环处理
for (int i = 0; i < OutputCount; i++)
{
// 计算误差
Errors[i] = expects[i] - Outputs[i];
}
}
public void Forward()
{
#if DEBUG
Debug.Assert(Inputs != null);
Debug.Assert(Outputs != null);
Debug.Assert(Hiddens != null);
Debug.Assert(InputBiases != null);
Debug.Assert(InputWeights != null);
Debug.Assert(OutputBiases != null);
Debug.Assert(OutputWeights != null);
#endif
// 计算隐藏层数据
for (int i = 0;i < HiddenCount;i ++)
{
// 数值
double value = 0.0;
// 循环处理
for(int j = 0;j < InputCount;j ++)
{
value += InputWeights[i][j] * Inputs[j];
}
// 设置输出值
Hiddens[i] = Sigmoid(value + InputBiases[i]);
}
// 计算输出层数据
for(int i = 0;i < OutputCount;i ++)
{
// 数值
double value = 0.0;
// 循环处理
for (int j = 0; j < HiddenCount; j++)
{
value += OutputWeights[i][j] * Hiddens[j];
}
// 设置输出值
Outputs[i] = Sigmoid(value + OutputBiases[i]);
}
}
public void Backword()
{
#if DEBUG
Debug.Assert(Errors != null);
Debug.Assert(Deltas != null);
Debug.Assert(Inputs != null);
Debug.Assert(Outputs != null);
Debug.Assert(Hiddens != null);
Debug.Assert(InputBiases != null);
Debug.Assert(InputWeights != null);
Debug.Assert(OutputBiases != null);
Debug.Assert(OutputWeights != null);
#endif
// 计算隐层
for (int i = 0;i < OutputCount;i ++)
{
// 链式反应
double delta = - Errors[i];
// 链式反应
delta *= DeltaSigmoid(Outputs[i]);
// 设置误差
Deltas[i] = delta;
// 设置新的偏置
// 与学习率有关
OutputBiases[i] -= LearningRate * delta;
// 循环处理
for (int j = 0;j < HiddenCount;j ++)
{
// 设置新的权重
// 与学习率有关
OutputWeights[i][j] -= LearningRate * delta * Hiddens[j];
}
}
// 计算输入层
for(int i = 0;i < HiddenCount;i ++)
{
// 链式反应
double delta = 0.0f;
// 循环处理
for (int j = 0;j < OutputCount;j ++)
{
// 链式反应
delta += OutputWeights[j][i] * Deltas[j];
}
// 链式反应
delta *= DeltaSigmoid(Hiddens[i]);
// 与学习率有关
// 设置新的偏置
InputBiases[i] -= LearningRate * delta;
// 循环处理
for(int j = 0;j < InputCount; j ++)
{
// 设置新的权重
// 与学习率有关
InputWeights[i][j] -= LearningRate * delta * Inputs[j];
}
}
}
public bool ImportFile(string fileName)
{
#if DEBUG
Debug.Assert(!string.IsNullOrEmpty(fileName));
#endif
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "开始输入数据!");
try
{
// 创建文件流
FileStream fs = new FileStream(fileName, FileMode.Open);
// 创建输出流
BinaryReader br = new BinaryReader(fs);
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "文件流已开启!");
// 读取标识符
string version = br.ReadString();
// 检查结果
if(string.IsNullOrEmpty(version) || !version.Equals("BPNetwork"))
{
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "无法识别的文件!");
return false;
}
// 读取InputCount;
InputCount = br.ReadInt32();
// 读取OutputCount;
OutputCount = br.ReadInt32();
// 读取HiddenCount;
HiddenCount = br.ReadInt32();
// 读取LearningRate;
LearningRate = br.ReadDouble();
// 初始化
Initialize(InputCount, OutputCount, HiddenCount);
#if DEBUG
Debug.Assert(Errors != null);
Debug.Assert(Deltas != null);
Debug.Assert(Inputs != null);
Debug.Assert(Outputs != null);
Debug.Assert(Hiddens != null);
Debug.Assert(InputBiases != null);
Debug.Assert(InputWeights != null);
Debug.Assert(OutputBiases != null);
Debug.Assert(OutputWeights != null);
#endif
// 输入数据
for (int i = 0; i < InputCount; i++)
{
InputBiases[i] = br.ReadDouble();
}
// 输入数据
for (int i = 0; i < HiddenCount; i++)
for (int j = 0; j < InputCount; j++)
{
InputWeights[i][j] = br.ReadDouble();
}
// 输入数据
for (int i = 0; i < OutputCount; i++)
{
OutputBiases[i] = br.ReadDouble();
}
// 输入数据
for (int i = 0; i < OutputCount; i++)
for (int j = 0; j < HiddenCount; j++)
{
OutputWeights[i][j] = br.ReadDouble();
}
// 关闭文件流
fs.Close();
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "文件流已关闭!");
}
catch (System.Exception ex)
{
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "unexpected exit !");
LogTool.LogMessage(string.Format("\texception.message = {0}", ex.Message));
// 返回结果
return false;
}
// 记录日志
LogTool.LogMessage("BPNetwork", "ImportFile", "数据输出完毕!");
// 返回结果
return true;
}
public void ExportFile(string fileName)
{
#if DEBUG
Debug.Assert(!string.IsNullOrEmpty(fileName));
#endif
// 记录日志
LogTool.LogMessage("BPNetwork", "ExportFile", "开始输出数据!");
try
{
// 保存至本地磁盘
// 创建文件流
FileStream fs = new FileStream(fileName, FileMode.Create);
// 创建输出流
BinaryWriter bw = new BinaryWriter(fs);
// 记录日志
LogTool.LogMessage("BPNetwork", "ExportFile", "文件流已开启!");
// 输出数据
bw.Write("BPNetwork");
bw.Write(InputCount);
bw.Write(OutputCount);
bw.Write(HiddenCount);
bw.Write(LearningRate);
#if DEBUG
Debug.Assert(Errors != null);
Debug.Assert(Deltas != null);
Debug.Assert(Inputs != null);
Debug.Assert(Outputs != null);
Debug.Assert(Hiddens != null);
Debug.Assert(InputBiases != null);
Debug.Assert(InputWeights != null);
Debug.Assert(OutputBiases != null);
Debug.Assert(OutputWeights != null);
#endif
// 输出数据
for (int i = 0; i < InputCount; i++) bw.Write(InputBiases[i]);
for (int i = 0; i < HiddenCount; i++)
for (int j = 0; j < InputCount; j++) bw.Write(InputWeights[i][j]);
// 输出数据
for (int i = 0; i < OutputCount; i++) bw.Write(OutputBiases[i]);
for (int i = 0; i < OutputCount; i++)
for (int j = 0; j < HiddenCount; j++) bw.Write(OutputWeights[i][j]);
// 刷新打印流
bw.Flush();
// 关闭打印流
bw.Close();
// 关闭文件流
fs.Close();
// 记录日志
LogTool.LogMessage("BPNetwork", "ExportFile", "文件流已关闭!");
}
catch (System.Exception ex)
{
// 记录日志
LogTool.LogMessage("BPNetwork", "ExportFile", "unexpected exit !");
LogTool.LogMessage(string.Format("\texception.message = {0}", ex.Message));
}
// 记录日志
LogTool.LogMessage("BPNetwork", "ExportFile", "数据输出完毕!");
}
public void Print()
{
#if DEBUG
Debug.Assert(Errors != null);
Debug.Assert(Deltas != null);
Debug.Assert(Inputs != null);
Debug.Assert(Outputs != null);
Debug.Assert(Hiddens != null);
Debug.Assert(InputBiases != null);
Debug.Assert(InputWeights != null);
Debug.Assert(OutputBiases != null);
Debug.Assert(OutputWeights != null);
#endif
LogTool.LogMessage("BPNetwork", "Print",
"打印数据!");
LogTool.LogMessage("\tInputCount = " + InputCount);
LogTool.LogMessage("\tOutputCount = " + OutputCount);
LogTool.LogMessage("\tHiddenCount = " + HiddenCount);
LogTool.LogMessage("\tLearningRate = " + LearningRate);
// 打印输入端数据
for (int i = 0; i < HiddenCount; i++)
LogTool.LogMessage(
string.Format("\tInputBiases[{0}] = {1}", i, InputBiases[i]));
for (int i = 0; i < HiddenCount; i++)
for(int j = 0;j < InputCount; j ++)
LogTool.LogMessage(
string.Format("\tInputWeights[{0}][{1}] = {2}", i,j, InputWeights[i][j]));
// 打印输出端数据
for (int i = 0; i < OutputCount; i++)
LogTool.LogMessage(
string.Format("\tOutputBiases[{0}] = {1}", i, OutputBiases[i]));
for (int i = 0; i < OutputCount; i++)
for (int j = 0; j < HiddenCount; j++)
LogTool.LogMessage(
string.Format("\tInputWeights[{0}][{1}] = {2}", i, j, OutputWeights[i][j]));
}
#if _USE_CONSOLE
public static void Main(string[] args)
{
// 开启日志
LogTool.SetLog(true);
// 创建计时器
Stopwatch watch = new Stopwatch();
// 开启计时器
watch.Start();
// 生成神经网络
BPNetwork network = new BPNetwork();
// 初始化
network.Initialize(2, 2, 2);
// 设置学习率
network.LearningRate = 0.5;
// 设置标定用值
double[] Inputs = new double[2] { 0.1, 0.2 };
double[] expects = new double[2] { 0.01, 0.99 };
// 设置输入权重
network.InputWeights = new double[][]
{
// W1和W2
new double[] { 0.1, 0.2 },
// W3和W4
new double[] { 0.3, 0.4 },
};
// 设置输出权重
network.OutputWeights = new double[][]
{
// W5和W6
new double[] { 0.5, 0.6 },
// W7和W8
new double[] { 0.7, 0.8 },
};
// 设置输入偏置
network.InputBiases = new double[] { 0.55, 0.56 };
// 设置输出偏置
network.OutputBiases = new double[] { 0.66, 0.67 };
// 设置输入值
network.SetInputs(Inputs);
// 计算一次正向传播
network.Forward();
// 获得输出值
double[] Outputs = network.GetOutputs();
// 打印输出值
//Outputs[0] = 0.7989476413779711
//Outputs[1] = 0.8390480283342561
Console.WriteLine("\toutputs[0] = " + Outputs[0]);
Console.WriteLine("\toutputs[1] = " + Outputs[1]);
// 设置预期数值
network.SetOutputs(expects);
// 打印误差
//error = 0.3226124392928197
Console.WriteLine("\terror = " + network.GetError());
// 计算一次反向传播
network.Backword();
// 关闭计时器
watch.Stop();
// 打印结果
Console.WriteLine(string.Format("Time elapsed : {0} ms ", watch.ElapsedMilliseconds));
}
#endif
}
}