Algorithm.Main(args[])

孤独的美食家

投影方差分割

作者在这里要介绍一种点集的分割算法（源自作者读《图像局部不变性特征与描述》时的一点灵感）。其起源来自于Kd树算法，但比Kd树算法更具有一般性。有关Kd树算法，会在文章开头做个简单介绍，并指出其中的起源点和关键点。

知乎：点集分割算法——基于投影方差分割

Kd树算法

在图形特征点匹配算法中，Kd树是一种常用的特征匹配算子。Kd树是英文K-dimension tree的缩写，是对数据点在\(k\)维空间中划分的一种数据结构。这里先以一个简单直观的示例来介绍Kd树算法，并找出其中的起源点和关键点。

图1 二维数据Kd树控件划分示意图

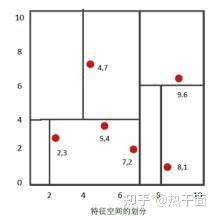
假设有6个二维数据点：\( \{ (2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\} \) 。数据点位于二维空间内，如图1所示。为了能有效地找到最近邻，Kd树采用分而治之的思想，即将空间划分成几个小部分。首先粗直线将空间一分为二，然后在两个子空间中，细直线又将整个空间划分为四个部分，最后虚直线将这四部分进一步划分。

Kd树构建的关键点就在于区间划分的标准：统计数据点在每个维度上的数据方差。挑选出方差中的最大值，对应的维就是分割域的值。还是以上面的实际例子为例：数据点是平面数据点，因此有两个维度。可以分别统计这些数据点在\(x\)轴和\(y\)轴上的数据方差。如果\(x\)轴方差较大，那么就以垂直于\(x\)轴方向划一条竖直线将空间一分为二；如果\(y\)轴方差较大，那么就以垂直于 \(y\)轴方向划一条水平线将空间一分为二。

Kd树中的两个维度是确定为\(x\)轴和\(y\)轴。从纯数学角度来看，这个平面点集的方差最大值未必就在\(x\)轴或\(y\)轴上。以此思路为核心进一步扩展：对于任一的多维度点集，求一条多维度直线，使得这些多维度点在这条直线上的投影点方差达到最大值。那么分割域的分割平面，就是垂直于该直线的平面。这条直线和这个平面是否存在且唯一在呢？

投影方差分割

按照不同维度可以逐步推导出投影方差的数学含义。

AlgMain : 一维投影方差分割
AlgMain : 二维投影方差分割
AlgMain : 三维投影方差分割
AlgMain : 多维投影方差分割

形象一点的解释就是：用一个“紧凑”的椭球（或者椭圆）去容纳（或覆盖）这些点，那么这个椭球（或椭圆）的最长轴所指方向就是使得距离方差达到最大值的方向，垂直于该方向且过椭球（或椭圆）中心的平面（或直线）就是分割平面（或直线）。

投影方差分割的特点

方差分割具有以下几个典型特点：

  • 平移不变性
  • 旋转不变性
  • 缩放不变性

对点集的平移、旋转和缩放，不影响方差分割方法。只有当点集的分布有明显变化时，方差分割才会发生改变。

投影方差分割的例子

下面给出几个方差分割的例子（基于Matlab）：

图4 二维点群方差分割

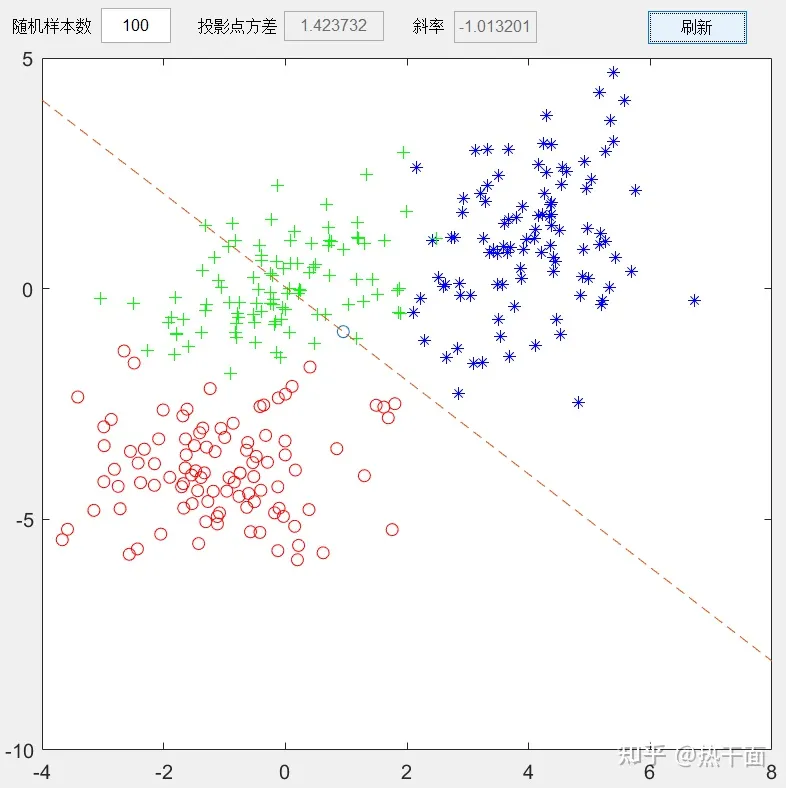
方差分割可以连续多次使用。将原有已分割平面进行进一步细分。每多进行一次分割，方差就会进一步缩减。另外，这种连续的方差分割，最后一定是凸分割。

这个证明思路其实也很简单：假设分割区域存在凹陷部分，那么必然就有突出点伸入到凹陷部分。由于封闭区域内距离方差小于一定值，这些突出点之前就应当在之前被分配原封闭区域内。这就与算法的基本要求相矛盾。具体的证明留给读者思考。

图5 二维点群经过三次方差分割

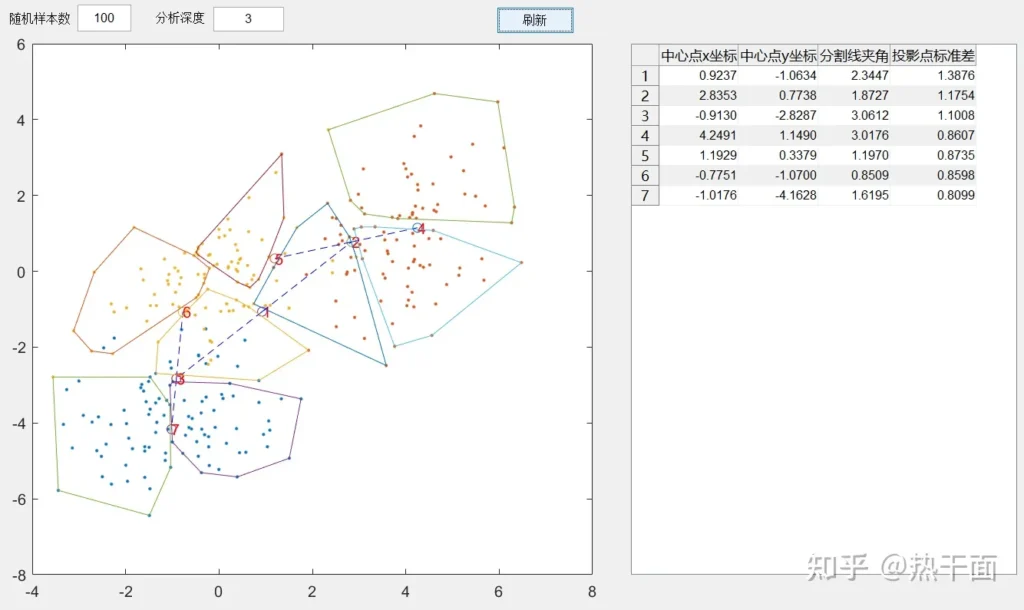
方差分割的结果某种意义上，可以形成一个图形的“特征值”。旋转，平移，缩放或者少量的增减，不会对这个“特征值”造成太大影响。

图6 对汉字点群经过三次方差分割

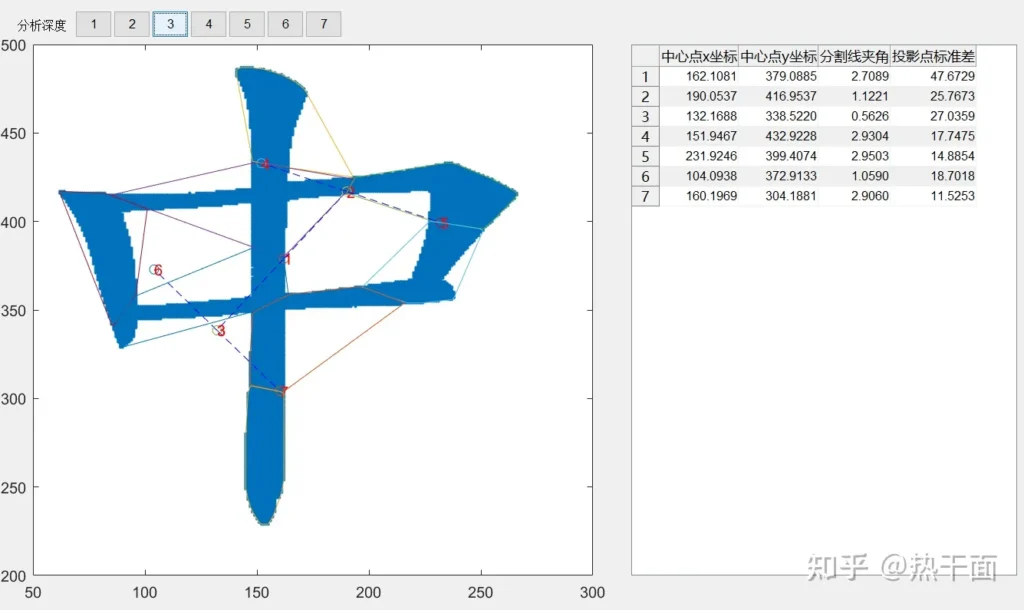
更加有意思的是：作者在阅读《数字图像处理的MATLAB实现（第二版）》时，发现在章节6.6—直接在RGB矢量空间中处理，其中的公式和二维分割算法几乎一样。有兴趣的读者可以查阅一下。

参考代码(Matlab)

function [xMean,yMean,beta,deviation] = MinVarianceSplit(xValues,yValues)
    %预处理检测
    count = length(xValues);
    if count <= 0
        fprintf('输入的数组没有元素！\n');
        return;
    end
    if count ~= length(yValues)
        fprintf('输入的X，Y数组长度不一致！\n');
        return;
    end
    %求X，Y平均值
    xMean = mean(xValues);
    yMean = mean(yValues);
    %平移所有点至中心点位置
    xNewValues = xValues - xMean;
    yNewValues = yValues - yMean;
    %计算几个常用数值
    xyNewValue = xNewValues * yNewValues';
    xxNewValue = xNewValues * xNewValues';
    yyNewValue = yNewValues * yNewValues';
    %计算beta角度
    beta = atan(2 * xyNewValue / (xxNewValue - yyNewValue)) / 2;
    %计算二阶导数判别式
    delta = - 2 * (xyNewValue * sin(2 * beta) + (xxNewValue - yyNewValue) * cos(2 * beta));
    %检查判别式
    if delta < 0
        %二阶导数小于零，说明是极大值
        %另外一个垂直方向就是极小值方向
        beta = beta + pi / 2.0;
    end
    %检查计算结果
    %调整输出方向在（0,pi）区间内
    if beta < 0
        beta = beta + pi;
    elseif beta > pi
        beta = beta - pi;
    end
    %计算投影点之间的方差数值
    deviation = sqrt((cos(2 * beta) * (xxNewValue - yyNewValue) + 2 * sin(2 * beta) * xyNewValue + (xxNewValue + yyNewValue)) / (2 * count));
end
Post Views: 164