摘要:给出了在微机上实现数控铣床加工仿真的两种有效途径。视向离散方法的主要思路是将毛坯和刀具进行离散,通过对离散后的数据结构进行一定操作来达到加工仿真的目的;三角片离散方法可以在仿真过程中不断地变换观察方式,而且仿真的结果能直接用于多种误差测量。
关键词:数控NC加工,NC加工仿真
- 《计算机辅助设计与图形学学报》2000年3月第12卷第3期——《在微机上实现数控铣床加工仿真》。
- 《计算机辅助设计与图形学学报》2001年11月第13卷第11期——《三角片离散法实现数控铣床加工仿真》。
1. 实现加工仿真的多种思路
近年来,随着CAD/CAM软件行业的发展,加工仿真软件脱颖而出。线切割、车床、铣床相继都有了相对应的仿真软件。其中的各种算法,特别是铣床的加工仿真算法,引起了广大同行们的兴趣。笔者从追求实时显示效果,到追求加工误差测量,到设计仿真平台,设计过多种仿真方案。本文结合作者的经验和对软件的研究,给广大同行们提供一些思路和想法。
1.1 线框法
线框法是一种十分简单而且容易实现的加工仿真方法,即在屏幕上以线框的方式画出加工刀具和零件模型。
当程序运行时,刀具不断地按显示的加工轨迹在屏幕上移动,加工仿真模块未对刀具和待加工毛坯进行数学处理,难以进行真实的铣削加工仿真。这种方法只能用于校验G代码有无明显错误,对于过切、余量只能通过眼睛的观察来判断,因此,这种方法很难称得上加工仿真。
真实感仿真是在此基础上加入过切判断机制,让刀具在零件的真实效果图上进行切削。如果过切,刀具就会把零件的真实效果图“切掉”一块。这种方法有所改进,但仍然不能显示整个真实的切削过程并对加工结果进行误差测量。
1.2 实体求减法
考虑到待加工毛坯一般为长方体,刀具可以由二次几何体拼凑而成。现在布尔实体造型技术已比较成熟,可以考虑用实体的差来实现加工仿真。
这种方法对待加工毛坯和刀具均采用标准的数学模型表示。进行加工仿真时,先求出刀具沿加工路径移动时所形成的扫描体,然后从毛坯中“减去”该扫描体,接着将结果进行真实感显示。
利用这种方法进行仿真,可以支持三轴和五轴加工。其加工出的零件表示具有连续性,可以放大或缩小显示,可以任意旋转视角,可以进行加工误差的测量。
但这种方法也存在一些问题:
- 对于加工代码少的零件比较适合,对于复杂零件其等待时间和数据量将大大增加;
- 求交过程和离散显示过程所消耗的时间将降低其实时性能;
- 求交过程中计算稳定性将影响整个仿真过程.从理论上讲,这种算法是最精确的加工仿真算法,不应当放弃深挖其潜力的研究。
1.3 视向离散法
现在大多数商业软件主要采用视向离散法。这种方法的主要思路是:将加工刀具和待加工毛坯沿视线方向上进行“等同”离散表示;然后在加工过程中,利用离散后的数据进行图像上的处理,以求达到真实的效果。
采用这样的方法可以达到很好的显示效果和实时性能,同时可以支持三轴和五轴加工。但其加工结果不具有连续性,不能放大或缩小显示,不能任意转动视角。除非改变视向后重新进行加工仿真 ;或者事先设置多个视角同时进行加工;或者利用该算法的特点:仅做一百八十度视角变换。利用加工仿真的结果可以确定加工中的过切、余量,进行截面观察和表面数据测量。
笔者利用这种思路完成了本科毕业论文。软件原型于1997年5月参加在北京举行的第5届国际机床展,改进版于同年7月参加在北京举行的全国CAD/CAM软件展。改进后的软件模块嵌入由北京华正模具研究所1998年4月2日所推出的计算机辅助设计和制造软件ME2.0中。
1.4 三角片离散法
追求显示效果和实时性能并不是唯一的目的,更主要的目的是进行加工结果误差测量。
这时考虑到三轴加工的特点,笔者提出轴向离散算法:把加工刀具和待加工毛坯沿刀轴方向等同离散表示。这种方法仅消除了视向离散方法中所存在的内存问题,其它问题仍未得到解决。
将这一方案进一步修改,就得到了近期所提出的三角片离散法:将待加工毛坯上表面用离散的三角片来表示。该方法不但具有视向离散的优点,而且简单易行,加工过程中可以不断地变换观察方式,通过简单的搜索来确定加工后的各种误差。
另外,可以加入机床和夹具一起进行仿真,达到真实仿真的效果。这种方法对显示要求较高,如果不采用显示技巧和快速显示硬件的支持,其实时性就较难保证。
2. 视向离散法
视向离散方法的基本思想是在等同离散的基础上处理物体的差。也就是将刀具和毛坯按屏幕分辨率离散成沿着视线方向的直线段。用组成刀具的直线段去裁剪组成毛坯的直线段以反映切削,加上对毛坯图像的处理就得到了切削的视觉效果。
应特别指出,在发生切削关系的某点处,刀具和毛坯相互接触;刀具上该点处的法矢和毛坯上该点处的法矢方向相反。对于平行透视下的平行光照模型,物体表面上法矢方向相同或相反处所计算得到的颜色值相同。因此,无需计算毛坯上这一点的颜色值,而只需将刀具上同一点的颜色值赋值给该点。
该方法首先利用光线跟踪算法,按屏幕分辨率将刀具和毛坯都离散成沿视线方向的直线段。沿视线方向的一条光线和刀具的交点不会多于两个,只能形成一条直线段;和毛坯的交点个数将随着毛坯复杂程度的变化而变化,可能会形成多条直线段,将多条这样的直线段串成一个链表结构。这样,离散后的刀具是由许多直线段组成,毛坯却是由许多直线段串成的链表组成。刀具和毛坯的整体切削关系变成离散直线段之间的切削关系。离散直线段之间的切削关系主要为刀具上的直线段和毛坯上的直线段链表的切削关系。最根本的切削关系为刀具上的直线段和毛坯上的直线段链表中的某一条直线段的6种切削关系。
由于这些直线段均沿着视线方向,因此在计算机屏幕上表现为一个点。当刀具上的直线段和毛坯上的直线段链表具有相同的屏幕坐标时,就有可能发生相互之间的切削关系。设刀具上有一直线段\(Q_1 Q_2\)和毛坯的一直线段链表对应屏幕上同一象素,\(P_1 P_2\)为该直线段链表的一个直线段单元。其中\(Q_1\)点离眼睛近,视向\(Z_{Q_1}\)值小;\(Q_2\)点离眼睛远,视向\(Z_{Q_2}\)值大。\(P_1\)点离眼睛近,视向\(Z_{P_1}\)值小;\(P_2\)点离眼睛远,视向\(Z_{P_2}\)值大。
第一种关系:\(Z_{P_2}>Z_{Q_2}>Z_{Q_1}>Z_{P_1}\)。如下面图(1)所示.可知直线段\(Q_1 Q_2\)的位置处于\(P_1 P_2\)之间,并将\(P_1 P_2\)切割为两段。

先申请一个链表直线段单元\(N_1 N_2\)。分别将\(Q_2\),\(P_2\)点的颜色值和视向\(Z\)值赋给\(N_1\),\(N_2\)点,并将该单元串到的后面。将\(Q_1\)点的颜色值和视向\(Z\)值赋给\(P_2\)点。
第二种关系:\(Z_{P_2} > Z_{Q_2} > Z_{P_1} > Z_{Q_1} \),如下图(2)所示。可知直线段\(Q_1 Q_2\)切削\(P_1 P_2\)的近端。

将\(Q_2\)点的颜色值和视向\(Z\)值赋给\(P_1\)点。如果直线段\(P_1 P_2\)为该链表的第一个单元,则应同时修改\(P_1\)点所对应屏幕点的颜色值。
第三种关系。\(Z_{P_2} >Z_{P_1} > Z_{Q_2} >Z_{Q_1}\),如下图(3)所示.可知直线段\(Q_1 Q_2\)与\(P_1 P_2\)没有发生切削关系。

第四种关系。\(Z_{Q_2}>Z_{P_2}>Z_{Q_1}>Z_{P_1}\),如下图(4)所示.可知直线段\(Q_1 Q_2\)切削\(P_1 P_2\)的远端。

将\(Q_1\)点的颜色值和视向\(Z\)值赋给\(P_2\)点。
第五种关系。\(Z_{Q_2}>Z_{Q_1}>Z_{P_2}>Z_{P_1}\),如下图(5)所示.可知直线段\(Q_1 Q_2\)与\(P_1 P_2\)没有发生切削关系。

第六种关系。\(Z_{Q_2}>Z_{P_2}>Z_{P_1}>Z_{Q_1}\),如下图(6)所示.可知直线段\(Q_1 Q_2\)切削\(P_1 P_2\)整条直线段。
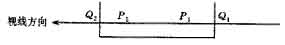
如果\(P_1 P_2\)为该链表的第一个单元,并且没有后继单元时,则删除该链表,并且将其所对应的屏幕点的颜色值改为背景色。当存在后继单元时,则删除该单元,并且将其所对应的屏幕点的颜色值改为后继单元的颜色。
以上为两线段之间的关系,全部切削关系需要对整个链表进行搜索判断后加以确定。只要能处理好以上六种关系,铣削加工仿真就能够很好地实现。
3 三角片离散法
三轴数控铣床加工有以下特点:
- 只有毛坯的上表面才是加工表面;
- 平行于刀轴的一条直线对与加工的毛坯的上表面的交点有且仅有一个(对于有通孔的零件也可以补上一张假想平面,使得毛坯上表面连续);
- 毛坯的上表面是通过每一点的不同高度来表达加工零件的表面形状。
因此,采用最简单的三角片离散法:将上表面离散为均匀点阵,再将这些点阵连接为三角片矩阵。程序运行时,不断地按照刀具路径修改上表面点阵的高度,再进行真实感渲染,就可以达到实时显示加工过程的效果。
图(7)是一个鼠标精加工的例子。该加工程序是一个鼠标精加工的走刀路径,一共有13768条直线指令。为了更好地理解该方法,现在选择毛坯的表面点阵密度较小,图(8)为线框图,图(9)为真实感图。当提高点阵密度时,效果会大大提高,见图(10)。




加工后的点阵中各点的横纵坐标值在加工期间不会改变,因此这些点仍然呈均匀分布。在加工过程中改变的仅是各点的高度值,因此相邻点间的不同高度值就体现了小区域内的形状特征。
通过一定的搜索和比较就能进行加工误差测量。例如,对平面度的测量,可以先给定一加工误差,搜索被鼠标点中的三角形邻近的点;当被搜索点的高度与指定的高度相差在误差范围内时,继续搜索,直到找到一个最大闭区域为止。其它误差的测量均可根据其特点和要求采取不同的搜索方式。